Solving the GCHQ christmas card with Python and pycosat

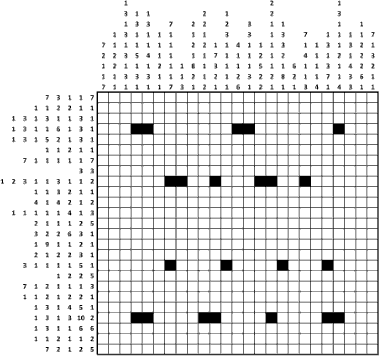
^{Copyright GCHQ. See the GCHQ post for the full image.}

Introduction

As you may have seen, Britain’s intelligence organization GCHQ has released a Christmas card featuring a grid-shading puzzle.

The puzzle is an instance of a Nonogram puzzle. This is a grid with numbers by each row and column, indicating the lengths of runs of shaded cells in the completed puzzle.

Instead of solving the problem by hand, I opted to write an automatic solver using Python and some rusty CS knowledge. The same script can be adapted to solve other Nonogram puzzles.

In this post I’ll explain how my script works, with the disclaimer that I don’t claim to be an expert in CNF or SAT solvers. This approach may not even be more efficient than a basic backtracking algorithm. Nevertheless, I found it an interesting exercise and hopefully you will too. Any feedback from SAT aficionados would also be much appreciated!

Full source code is available here.

SAT solvers

I decided to solve the problem by expressing it as a boolean formula in Conjunctive normal form (CNF) and feeding the result into a SAT solver. My reasons for doing this were as follows:

• The problem is NP-complete. As such I felt justified in reducing it to an instance of the satisfiability problem (also NP-complete).
• Other, ostensibly similar problems such as Sudoku are tersely expressibly in CNF.
• There’s an easy to use Python binding to the SAT solver picosat, in the form of pycosat.

So what exactly is CNF, and what is a SAT solver? In short, CNF is a way of writing a boolean formula, eg:

as series of ANDs of ORs, where NOTs may only appear directly applied to variables:

Each sequence of ORs is called a clause, and each element of the clause (ie. a possibly negated variable) is called a term. The whole CNF expression can therefore be seen as a sequence of clauses.

A SAT solver is a program which given a boolean formula in CNF, assigns truth values to the variables of the formula such that the formula is true. Each such assignment is a solution to the boolean satisfiability problem. Above,

is a solution, as is

for example.

is not a solution however.

In practice, CNF expressions have many thousands of terms. For example the Sudoku solver example from the picosat repository has 11,764 clauses, and 24,076 terms.

SAT solving algorithms have been the subject of intense competition over the past decade due to applications in AI, circuit design, and automatic theorem proving. As such we can leverage these advances just by expressing our problem as CNF.

Variables

So, we’re looking to map our puzzle into a CNF expression, with the idea that we’ll be able to read the truth assignments in any solution to determine which grid cells should be filled in. As such it would seem natural to introduce a variable \( shaded_{i,j} \)for each grid cell, which is true iff the corresponding cell should be filled in. In our case the grid is 25x25, so we’d have 625 such variables.

So what should the formula be? Let’s start off by writing our clauses out in English. In the below rules, a “row run” refers to a horizontal sequence of consecutive shaded cells, each of which corresponds with one of the numbers down the left hand side of the original puzzle. Similarly, a “column run” is a vertical sequence of shaded cells, corresponding with the numbers at the top of the puzzle. With that in mind, here are the rules:

1. A row run being in a particular position implies the corresponding cells are shaded.
2. The converse of the above: If a given cell is shaded, then there must be a row run that covers this cell.
3. A column run being in a particular position implies the corresponding cells are shaded.
4. The converse of the above: If a given cell is shaded, then there must be a column run that covers this cell.
5. A row run can be in at most one position.
6. A column run can be in at most one position.
7. A row run being in a particular position implies that the next row runs on the same row must appear after the first row run.
8. Same as above but for column runs.
9. Row runs and column runs must not be in invalid positions.
10. Any cells that are shaded in the problem (“givens”) must be shaded in the solution.

With the above in mind, it seems intuitive to introduce new variables \( rowrunpos_{i,j,k} \) and \( colrunpos_{i,j,k} \) with the following semantics:

• \( rowrunpos_{i,j,k} \) is true iff the \( j^{th} \) row run on row \( i \) starts at column \( k \).
• \( colrunpos_{i,j,k} \) is true iff the \( j^{th} \) column run on column \( i \) starts at row \( k \).

This means for each number around the edge of the puzzle we’ll have 25 new variables.

Introducing new variables helps constrain the size of the CNF while maintaining equivalence. See the Wikipedia page for CNF for an illustrative example.

The exact choice of where it is best to introduce variables is non-trivial and is beyond the scope of this post.

CNF clauses

With our variables established, we can now more or less directly translate the above English clauses into CNF clauses. Here’s the code for rule #1:

# A row run being present at a particular column implies the corresponding
# cells are shaded.
def row_run_implies_shaded():
    clauses = []
    for (row, run_idx, start_col), run_var in row_run_vars.items():
        run_len = ROW_RUNS[row][run_idx]
        for col in range(start_col,
                         min(start_col + run_len, WIDTH)):
            clauses.append([-run_var.idx, shaded_vars[row, col].idx])
    return clauses

This is encoding the expression:

Which by expanding the implication is equivalent to:

Here’s the first couple of clauses that the above function returns, with annotations:

[
  [
    -809, # NOT (Row,run 1,2 starts at col 8) OR
    34,   # (Shaded @ 1, 8)
  ] # AND 
  [
    -809, # NOT (Row,run 1,2 starts at col 8) OR
    35,   # (Shaded @ 1, 9)
  ] # AND 
  ...
]

The first of these clauses says “if the third run in the second row starts at column 8, then cell (1, 8) must be shaded”. There’s one clause for each cell in each possible position of each row run.

Some things to note about CNF expressions expected by pycosat:

• A CNF expression is a list of lists of integers (!= 0).
• Each variable in the formula is represented by an integer > 0. Negative numbers may appear in the expression, in which case they correspond with the logical NOT of the variable represented by the unnegated number.
• The inner lists represent an OR of the terms contained within that list.
• The outer list represents an AND of the clauses contained within.

In the above code, row_run_vars[row, run_idx, start_col] and shaded_vars[row, col] correspond with the variables \( rowrunpos_{i,j,k} \) and \( shaded_{i,k} \) respectively. Each variable is represented by a Var object (created by me) which exists to associate useful debug information (Var.__str__) with the opaque variable index (Var.idx).

ROW_RUNS encodes the numbers down the left hand side of the puzzle as a list of lists.

The remaining clauses follow a similar pattern of translation. See the source code for the full details. The resulting CNF expression has 307,703 clauses, and 637,142 terms.

Extracting the solution

Having pycosat solve the problem is simply a case of calling pycosat.solve():

solution = pycosat.solve(all_clauses)

The result encodes a single truth assignment:

• A list of integers (!= 0).
• There is one entry for each variable in the input CNF.
• As before, each integer corresponds with a variable.
• If the integer is negative then the corresponding variable is false in the solution, otherwise the variable is true in the solution.

It’s then just a case of mapping the integers back to variables, and displaying in grid form.

def pretty_print_solution(sol):
    true_var_indices = {t for t in sol if t > 0}
    for row in range(HEIGHT):
        print "".join(".#"[shaded_vars[row, col].idx in true_var_indices]
                                                       for col in range(WIDTH))
    print

And here is the result:

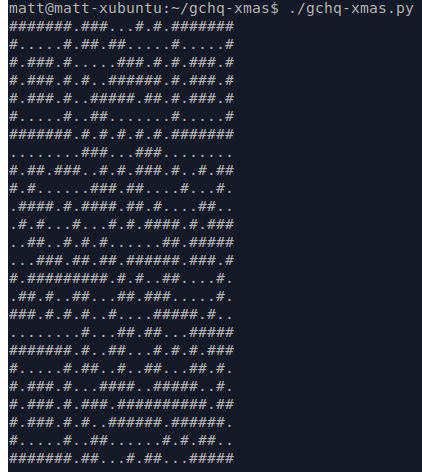
…a QR code which when decoded links you to the next stage in the puzzle.